
La synthèse d’une distribution statistique peut se faire de deux manières différentes :
- Utiliser des tableaux et des graphiques pour faire une synthèse visuelle
- Fournir un résumé numérique en calculant les paramètres statistiques
Ce chapitre examine les trois paramètres de tendance centrale que sont la moyenne, le mode et la médiane.
Les moyennes
La moyenne arithmétique :
La moyenne arithmétique, également appelée moyenne simple ou moyenne, est une mesure statistique qui est utilisée pour décrire la tendance centrale d’un ensemble de données numériques.
Elle est calculée en additionnant tous les nombres dans l’ensemble de données, puis en divisant la somme par le nombre total de nombres dans l’ensemble.
La formule pour calculer la moyenne arithmétique est la suivante : moyenne = (somme des valeurs ou des observations) / (nombre de valeurs ou des observations).
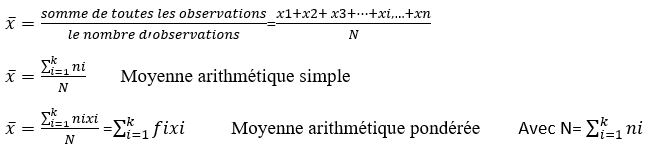
Par exemple, si vous aviez un ensemble de données contenant les nombres 2, 4, 6 et 8, vous pourriez calculer la moyenne arithmétique comme suit :
Moyenne = (2 + 4 + 6 + 8) / 4
= 20 / 4
= 5
Dans ce cas, la moyenne arithmétique de l’ensemble de données est 5. Cela signifie que 5 est une représentation approximative de la valeur centrale de l’ensemble de données.
Application : variable discrète
Calculer les moyennes arithmétiques des séries suivantes :
Soit la série de notes suivante : 2-6-12-10-12-10-10-6
Soit la série des notes de l’exercice qui peut être présentée de la manière suivante :
| xi | ni | xini |
|---|---|---|
| 2 | 1 | 2 |
| 6 | 2 | 12 |
| 10 | 3 | 30 |
| 12 | 2 | 24 |
| TOTAL | N=8 | 68 |
Application : variable continue
Soit la série suivante statistique de répartition des salariés selon l’âge
| Salaire | ni |
|---|---|
| [20-25[ [25-30[ [30-35[ [35-40[ [40-45[ [45-50[ | 8 10 20 25 15 10 |
| Total | 88 |
La moyenne géométrique :
La moyenne géométrique est une mesure de tendance centrale qui est calculée en prenant la racine nème du produit de n nombres.
Elle est souvent utilisée pour représenter la croissance moyenne d’un ensemble de valeurs ou pour calculer le taux de rendement moyen d’un investissement.
Plus formellement, si nous avons n nombres réels positifs x1, x2, …, xn, alors la moyenne géométrique est calculée comme suit :
Moyenne géométrique = (x1 * x2 * … * xn)^(1/n)
Par exemple, si nous avons les nombres 2, 4 et 8, la moyenne géométrique serait :
G = (2 * 4 * 8)^(1/3) = 4
Nous identifions G, la racine nième du produit de xini, comme la moyenne géométrique de la distribution, « (xi,ni)i varie entre 1 et k ».

Alors le log de la moyenne géométrique de la distribution {(xi,ni)1≤i≤k} n’est autre que la moyenne arithmétique de la distribution {(ln(xi),ni)1≤i≤k}.
Exemple : calculons la moyenne géométrique de 8, 5, 10
Exemple : calculer la moyenne géométrique de la série statistique suivante :
| xi | ni | fi | ln(xi) | fi*ln(xi) |
| 2 | 1 | 0,125 | 0,69 | 0,08625 |
| 6 | 2 | 0,25 | 1,8 | 0,45 |
| 10 | 3 | 0,375 | 2,3 | 0,8625 |
| 12 | 2 | 0,25 | 2,5 | 0,625 |
| 2,02375 |
La moyenne Harmonique :
La moyenne harmonique est une mesure statistique qui est utilisée pour calculer la moyenne d’un ensemble de nombres.
Elle est définie comme l’inverse de la moyenne des inverses des nombres dans l’ensemble. Autrement dit, si vous avez une série de nombres x1, x2, x3, …, xn, la moyenne harmonique est donnée par :
Moyenne harmonique = n / (1/x1 + 1/x2 + 1/x3 + … + 1/xn)

La moyenne harmonique est généralement utilisée pour calculer des moyennes dans des situations où des valeurs extrêmes ou des valeurs aberrantes sont présentes.
Elle est également utilisée en finance pour calculer des ratios tels que le ratio prix/bénéfice d’une entreprise.
Ainsi, on utilise cette moyenne dans le calcul des durées moyennes et des vitesses et aussi dans le calcul des moyennes de rapports et de pourcentages et dans le calcul de certain indice statistiques…
Il convient de noter que la moyenne harmonique est généralement inférieure à la moyenne arithmétique des mêmes nombres.
Cela est dû au fait que les nombres inverses sont souvent plus grands que les nombres eux-mêmes, et donc, la moyenne harmonique est affectée par les valeurs extrêmes plus que la moyenne arithmétique.
Exemple :
| xi | ni | ni/xi |
| 2 | 1 | 0,5 |
| 6 | 2 | 0,33 |
| 10 | 3 | 0,3 |
| 12 | 2 | 0,16 |
| 8 | 1,29 |
La moyenne quadratique :
La moyenne quadratique, notée Q, d’une distribution {(xi,ni)1≤i≤k} est la racine carrée de la moyenne arithmétique de la distribution {(xi2,ni)1≤i≤k}
Elle intervient dans le calcul certains paramètres de dispersion, à savoir les écarts types ou les
variances.

Exemple :
| xi | ni | xi² | nixi² |
| 2 | 1 | 4 | 4 |
| 6 | 2 | 36 | 72 |
| 10 | 3 | 100 | 300 |
| 12 | 2 | 144 | 288 |
| 8 | 664 |
Conclusion
Les moyennes quadratique, arithmétique, géométrique et harmonique sont toutes des mesures de tendance centrale qui peuvent être utilisées pour résumer un ensemble de données.
Voici une comparaison des quatre types de moyennes :
La moyenne Arithmétique
La moyenne arithmétique est la plus couramment utilisée et est calculée en additionnant toutes les valeurs d’un ensemble de données et en divisant le résultat par le nombre de valeurs. Elle donne une idée de la « valeur moyenne » de l’ensemble de données.
La moyenne Géométrique
La moyenne géométrique est calculée en multipliant toutes les valeurs d’un ensemble de données, puis en prenant la racine n-ième du produit, où n est le nombre de valeurs. Elle est souvent utilisée pour calculer des taux de croissance ou des rendements d’investissement moyens.
La moyenne Harmonique
La moyenne harmonique est calculée en prenant le nombre de valeurs dans un ensemble de données, en divisant ce nombre par la somme des inverses de chaque valeur, puis en prenant l’inverse du résultat. Elle est souvent utilisée pour calculer des moyennes
pondérées de taux ou de ratios.
La moyenne Quadratique
La moyenne quadratique est calculée en prenant la racine carrée de la moyenne arithmétique des carrés de chaque valeur dans un ensemble de données. Elle est souvent utilisée pour calculer des écarts types ou des variances.
Résumé
En résumé, chaque type de moyenne est utile dans des contextes différents. La moyenne arithmétique est la plus couramment utilisée, tandis que la moyenne géométrique est utile pour calculer des taux de croissance. La moyenne harmonique est utile pour calculer des moyennes pondérées de taux ou de ratios. Enfin, la moyenne quadratique est utile pour calculer des écarts types ou des variances.
Nous constatons que les quatre moyennes valident de manière cohérente l’ordre suivant pour des séries statistiques identiques :

La moyenne arithmétique présente l’inconvénient d’être très sensible aux valeurs extrêmes de la série. Celles-ci ont peu d’impact sur la moyenne géométrique. La moyenne harmonique est plus sensible aux petites valeurs de la série qu’à ses grandes valeurs.

Le mode
C’est la valeur du caractère le plus fréquent.
Cas d’une variable discrète :
Dans cette situation, le mode peut être rapidement déterminé à partir du tableau statistique ou du graphique (diagramme en bâtons).
| Série Unimodale | Série bimodale |
| 8 ; 9 ; 10 ; 12 ; 12 ; 12 ; 18 M0=12 | 2 ; 17 ; 17 ; 17 ; 17 ; 33 ; 33 ; 39 ; 39 ; 39 ; 39 ; 51 M01=17 M02=39 |
Cas d’une variable continue (amplitudes égales) :
| Salaires | ni |
|---|---|
| 10-15 | 9 |
| 15-20 | 25 |
| 20-25 | 32 |
| 25-30 | 16 |
| Total | 82 |
On peut prendre comme mode le centre de classe 22,5
On peut chercher à obtenir le mode avec plus de précision :
Détermination algébrique :

Cas d’une variable continue (amplitudes inégales) :
| Salaires | ni | ai | L=ai/ar | n’i=ni/L |
| 0-5 | 50 | 5 | 1 | 50 |
| 5-10 | 100 | 5 | 1 | 100 |
| 10-20 | 400 | 10 | 2 | 200 |
| 20-30 | 120 | 10 | 2 | 60 |
| 30-50 | 60 | 20 | 4 | 15 |

Détermination graphique :
On détermine le mode à l’aide d’un histogramme

La médiane (Me) :
La médiane est une mesure de tendance centrale qui divise une distribution en deux parties égales.
Elle correspond à la valeur qui sépare la moitié supérieure des données de la moitié inférieure.
Pour calculer la médiane, il faut trier les données par ordre croissant ou décroissant, puis prendre la valeur centrale ou la moyenne des deux valeurs centrales si le nombre de données est pair.
Par exemple, si on a les données suivantes : 2, 5, 7, 8, 10, la médiane est 7, car elle sépare les valeurs 2, 5 et 7 qui sont dans la moitié inférieure, des valeurs 8 et 10 qui sont dans la moitié supérieure.
Si on a les données suivantes : 2, 5, 7, 8, 10, 11, la médiane est 7,5 car c’est la moyenne des deux valeurs centrales, 7 et 8, qui divisent les données en deux parties égales.
Variable discrète :
Série à un nombre impair
Etape 1 : Classer la série 75 62 57 12 18
Etape 2 : Calculer le rang N+1/2=3
Etape 3 : Me= valeur du rang 3 Me=57
Série à un nombre pair
Etape 1 : Classer la série 12 25 32 44 52 69
Etape 2 : Calculer le 1er rang N/2=3
Etape 3 : Calculer le 2ème rang 1+N/2=4
Étape 4 : Me=la moyenne des deux rangs (32+44)/2= 38
Variable continue :
| Salaires | ni |
|---|---|
| 10-15 | 9 |
| 15-20 | 25 |
| 20-25 | 32 |
| 25-30 | 16 |
| Total | 82 |
Étape 2 : Déterminer la classe de Me :
Il s’agit de trouver la classe à laquelle appartient le 41ᵉ individu, pour cela, on classe les individus par ordre croissant des salaires, ce qui revient à construire la colonne des effectifs cumulés.
Me ∈ [20-25], on peut calculer avec plus de précision Me en faisant une interpolation linéaire.
Étape 3 : Interpolation linéaire
On connaît les salaires des 34 individus est 20 et les salaires des 66 individus est 25
34<41<66
20<Me<25

Alors 50% de la population ont un salaire inférieur à 21,09 dh et 50% ont en plus
Détermination graphique de la médiane :
On détermine la médiane à l’aide de la courbe cumulative





[…] · Histogramme : 1er cas (Amplitudes égales) […]
[…] travailler efficacement cette série de statistique descriptive sur les paramètres de tendance centrale [les Moyennes, le Mode la Médiane] il est essentiel de se référer au cours avant de commencer […]
[…] et pour évaluer la façon dont les données sont réparties autour de la mesure de tendance centrale, telle que la moyenne ou la […]
[…] ∆M=ML– Me […]